Hukum Kekekalan Energi
Hukum Kekekalan Energi – Pengantar
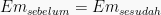
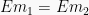 Maka persamaan diatas dapat dijabarkan sebagai:
Maka persamaan diatas dapat dijabarkan sebagai:
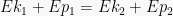
 Karena kekekalan energi merupakan sebuah hukum, maka bagaimanapun
caranya persamaan di sebelah kiri harus selalu sama dengan persamaan di
sebelah kanan. Dengan cara inilah, para insinyur dapat merancang dan
memprediksi mesin-mesin daya seperti turbin air dan generator yang mampu
mengubah energi potensial air menjadi energi kinetik kemudian
mengubahnya menjadi energi listrik, juga mesin mobil yang mampu mengubah energi kimia menjadi energi kinetik.
Karena kekekalan energi merupakan sebuah hukum, maka bagaimanapun
caranya persamaan di sebelah kiri harus selalu sama dengan persamaan di
sebelah kanan. Dengan cara inilah, para insinyur dapat merancang dan
memprediksi mesin-mesin daya seperti turbin air dan generator yang mampu
mengubah energi potensial air menjadi energi kinetik kemudian
mengubahnya menjadi energi listrik, juga mesin mobil yang mampu mengubah energi kimia menjadi energi kinetik.

Selain itu, sebagian energi kinetik yang terbentuk hilang karena gesekan pada piston mesin atau hilang karena hambatan lain. Sehingga, hanya sebagian kecil dari total energi awal pada mobil yang digunakan murni untuk menggerakkan mobil (hanya sekitar 15%). Energi-energi yang tidak termanfaatkan tersebut disebut kerugian-kerugian. Kerugian-kerugian tersebut tidak menghilangkan energi, akan tetapi mengubah energi menjadi bentuk yang tidak dapat dimanfaatkan, dan hal ini tak dapat terelakkan.


 Astronot Alan Shepard saat berada di bulan memukul bola golf secara
vertikal ke atas dari permukaan bulan yang memiliki percepatan gravitasi
sebesar 1,6 m/s2. Bola tersebut diketahui melaju dengan kecepatan 28 m/s. Seberapa tinggi bola golf dapat naik?
Astronot Alan Shepard saat berada di bulan memukul bola golf secara
vertikal ke atas dari permukaan bulan yang memiliki percepatan gravitasi
sebesar 1,6 m/s2. Bola tersebut diketahui melaju dengan kecepatan 28 m/s. Seberapa tinggi bola golf dapat naik?
Pembahasan:
Diketahui bahwa:
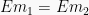
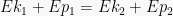
 Pada saat awal, bola masih berada di permukaan maka ketinggiannya
nol, kecepatan awalnya pun sama dengan nol. Sehingga persamaannya
menjadi:
Pada saat awal, bola masih berada di permukaan maka ketinggiannya
nol, kecepatan awalnya pun sama dengan nol. Sehingga persamaannya
menjadi:
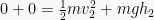
 sehingga,
sehingga,
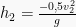
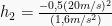
 Tanda minus menunjukkan arahnya. Pada kasus ini, tanda minus menunjukkan arah ke atas.
Tanda minus menunjukkan arahnya. Pada kasus ini, tanda minus menunjukkan arah ke atas.
(A) 13 cm
(B) 27 cm
(C) 31 cm
(D) 42 cm
(E) 47 cm
Pembahasan
Peristiwa diatas merupakan tumbukan. Peristiwa tumbukan sebenarnya merupakan peristiwa dimana dua benda saling memberikan aksi satu sama lain dalam waktu yang singkat. Karena gaya-gaya bekerja dalam waktu yang sangat singkat maka kita tidak bisa mengamati keadaan sistem pada saat kedua benda saling berinteraksi. Dengan demikian, akan lebih mudah jika benda dianalisis pada keadaan sebelum dan sesudah tumbukan terjadi.
Momentum didefinisikan sebagai perkalian antara massa sebuah benda dengan kecepatan geraknya:
Momentum merupakan besaran vektor. Jadi, arah gerak benda mempengaruhi tanda (+) dan (-) pada saat melakukan perhitungan.
Persamaan terakhir dari hukum Newton II menyatakan bahwa gaya yang
bekerja dalam selang waktu Δt menghasilkan perubahan momentum sebesar
mΔv. Besaran FΔt disebut impuls. Impuls biasanya disimbolkan dengan
huruf I.
Tumbukan yang terjadi pada soal diatas merupakan tumbukan non-elastis sempurna karena kedua benda menyatu setelah proses tumbukan. Pada tumbukan non-elastis sempurna, momentumnya konstan dan energi kinetiknya TIDAK kekal.

 (non-elastis sempurna)
(non-elastis sempurna)



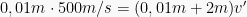
 (arah vektor ke atas)
(arah vektor ke atas)
Pada saat kedua benda bertumbukan, proses tumbukan terjadi secara vertikal (tegak lurus), Energi Potensial tidak bisa diabaikan seperti pada proses tumbukan horizontal. Oleh karena itu, digunakan sistem kekekalan energi mekanik.
Dalam kasus ini pada saat kedua benda bertumbukan, karena arah gaya yang disebabkan kecepatan (keatas) berlawanan dengan arah gaya berat yang selalu kebawah, maka arah gaya energi kinetik berlawanan dengan energi potensial, sehingga:

 Kecepatan akhir
Kecepatan akhir  dan
dan  merupakan ketinggian tumbukan balok dan peluru maksimum. Sedangkan, untuk kecepatan awal
merupakan ketinggian tumbukan balok dan peluru maksimum. Sedangkan, untuk kecepatan awal  sama dengan 0 karena pada saat
sama dengan 0 karena pada saat  (ketinggian awal balok yakni ketika balok masih diatas meja), balok dan
peluru masih belum bertumbukan sehingga balok dianggap belum bergerak.
Maka:
(ketinggian awal balok yakni ketika balok masih diatas meja), balok dan
peluru masih belum bertumbukan sehingga balok dianggap belum bergerak.
Maka:

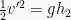

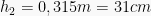 Jawaban: (C)
Jawaban: (C)
Kekekalan artinya tidak berubah. Jadi, hukum kekekalan energi
merupakan hukum yang menyatakan bahwa energi itu kekal dan tidak dapat
berubah (besarnya) sepanjang waktu, memiliki nilai yang sama baik
sebelum sesuatu terjadi maupun sesudahnya. Energi dapat diubah
bentuknya, tapi besarnya akan selalu sama.
Energi disini ialah total energi dari suatu sistem. Total energi dari suatu sistem dapat berupa energi kinetik, energi potensial,
energi panas, dan lain sebagainya. Bentuk-bentuk energi tersebut dapat
berupah menjadi bentuk energi lainnya sehingga total energi pada suatu
sistem akan selalu sama.Energi Mekanik
Energi mekanik merupakan jumlah dari energi kinetik dan energi potensial.
Em = Ek + Ep
Karena hukum kekekalan energi mengatur bahwa setiap total energi pada
sistem (yakni energi mekanik) harus selalu sama, maka energi mekanik
sebelum dan sesudahnya memiliki besar yang sama.Contoh Penerapan Hukum Kekekalan Energi
Pembangkit Listrik tenaga Hidro
Pada bendungan (dam) pembangkit listrik tenaga hidro, air dibendung hingga mencapai ketinggian (h) yang tinggi sehingga air di waduk memiliki energi potensial yang tinggi. Air masuk dari pintu air melewati jalur air hingga ke turbin dan memutar turbin. Energi potensial air kemudian berubah menjadi energi kinetik pada turbin sehingga turbin berputar. Karena turbin berputar, maka generator pun ikut berputar. Energi kinetik pada turbin kemudian berubah menjadi energi listrik pada generator. Listrik dari generator kemudian dialirkan melalui kabel tegangan tinggi jarak jauh. Energi listrik inilah yang kita nikmati sehari-hari.
Gambar. Skema bendungan air pada pembangkit listrik tenaga hidro
Mobil atau Kendaraan Bermotor
Pada mobil atau kendaraan bermotor, prinsipnya selalu sama. Energi kimia yang terdapat dalam bahan bakar diubah menjadi energi kinetik pada mesin mobil. Energi kinetik tersebutlah yang menggerakkan mobil. Besarnya energi kinetik yang menggerakkan mobil lebih kecil dari besarnya energi kimia pada bahan bakar. Hal ini disebabkan karena tidak seluruh energi kimia berubah menjadi energi kinetik. Sebagian besar energi yang tidak berubah menjadi energi kinetik tersebut, akan tetapi berubah menjadi energi dalam bentuk lain seperti panas, getaran, dan lain-lain.Selain itu, sebagian energi kinetik yang terbentuk hilang karena gesekan pada piston mesin atau hilang karena hambatan lain. Sehingga, hanya sebagian kecil dari total energi awal pada mobil yang digunakan murni untuk menggerakkan mobil (hanya sekitar 15%). Energi-energi yang tidak termanfaatkan tersebut disebut kerugian-kerugian. Kerugian-kerugian tersebut tidak menghilangkan energi, akan tetapi mengubah energi menjadi bentuk yang tidak dapat dimanfaatkan, dan hal ini tak dapat terelakkan.

Teko Pemanas Air
Pada saat kita menggunakan teko pemanas air, kita sebenarnya melihat prinsip kekekalan energi. Teko pemanas air mengubah energi listrik dari kabel menjadi energi panas pada element pemanas. Elemen pemanas inilah yang kemudian memanaskan air sehingga energi panas berpindah ke air pada teko. Terdapat pula beberapa kerugian-kerugian energi yang hilang dalam bentuk panas ke lingkungan, suara, dan lain-lain.
Gambar. Teko pemanas air
Contoh Soal Hukum Kekekalan Energi
Contoh Soal 1

Pembahasan:
Diketahui bahwa:
Contoh Soal 2
(SIMAK UI 2013) Sebuah balok ditembak pada arah vertikal dengan sebuah peluru yang memiliki kecepatan 500 m/s. Massa peluru 10 gr, sedangkan massa balok 2 kg. Setelah ditembakkan, peluru bersarang di dalam balok. Balok akan terpental ke atas hingga ketinggian maksimum ….(A) 13 cm
(B) 27 cm
(C) 31 cm
(D) 42 cm
(E) 47 cm
Pembahasan
Peristiwa diatas merupakan tumbukan. Peristiwa tumbukan sebenarnya merupakan peristiwa dimana dua benda saling memberikan aksi satu sama lain dalam waktu yang singkat. Karena gaya-gaya bekerja dalam waktu yang sangat singkat maka kita tidak bisa mengamati keadaan sistem pada saat kedua benda saling berinteraksi. Dengan demikian, akan lebih mudah jika benda dianalisis pada keadaan sebelum dan sesudah tumbukan terjadi.
Momentum didefinisikan sebagai perkalian antara massa sebuah benda dengan kecepatan geraknya:
p = mv
p = momentum (kg m/s) ; m = massa benda (kg); v = kecepatan benda (m/s)Momentum merupakan besaran vektor. Jadi, arah gerak benda mempengaruhi tanda (+) dan (-) pada saat melakukan perhitungan.
I = FΔt
Impuls merupakan besaran vektor.Tumbukan yang terjadi pada soal diatas merupakan tumbukan non-elastis sempurna karena kedua benda menyatu setelah proses tumbukan. Pada tumbukan non-elastis sempurna, momentumnya konstan dan energi kinetiknya TIDAK kekal.
momentum awal = momentum akhir
Pada saat kedua benda bertumbukan, proses tumbukan terjadi secara vertikal (tegak lurus), Energi Potensial tidak bisa diabaikan seperti pada proses tumbukan horizontal. Oleh karena itu, digunakan sistem kekekalan energi mekanik.
Dalam kasus ini pada saat kedua benda bertumbukan, karena arah gaya yang disebabkan kecepatan (keatas) berlawanan dengan arah gaya berat yang selalu kebawah, maka arah gaya energi kinetik berlawanan dengan energi potensial, sehingga:
ΔEk = ΔEp






0 komentar:
Posting Komentar